
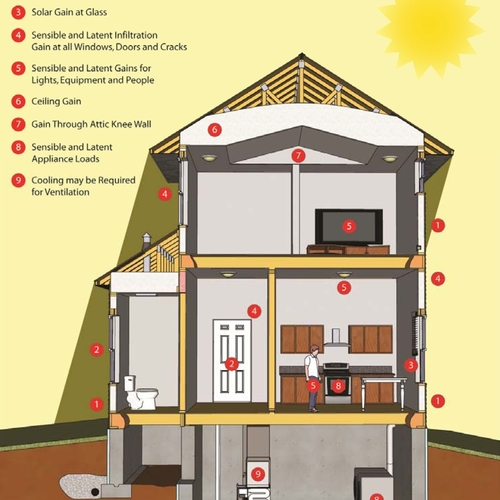
Image Credit: Energy Vanguard
When you embark on the project of educating yourself about building science, one of the first things you encounter is the concept of heating and cooling loads. Every building has them. (Yes, even Passive House projects.) That’s why we do heating and cooling load calculations. We enter all the details of the building, set the design conditions, and get the heating and cooling loads for each room in the building. Here in the US we still use those antiquated units that yield British Thermal Units per hour (BTU/hr) for the loads. In most of the world, the result is measured in watts of kilowatts.
But then what? We don’t just turn on the BTU spigot. We move those BTUs into and out of the rooms in a house with a fluid, typically air or water. So how do we know how many cubic feet per minute (cfm) of air will give us the right number of BTUs per hour? Well, today we’re going to do a tiny bit of math and talk about this relationship between BTU/hr and cfm. (I’m going to leave the discussion of using water for heat distribution to my friends on the hydronic side, but it’s analogous to what I’m explaining below.)
How much heat can air hold?
Matter is pretty neat stuff. It has all kinds of interesting properties that have kept scientists hidden away in laboratories for centuries. (I hear that Galileo is still toiling away in the basement of the Leaning Tower of Pisa.) When talking about the capacity of air to hold heat, the relevant property is called — you’re not gonna believe it — heat capacity. Yep. It’s a term I’ve mentioned occasionally in this space but never really defined, so let’s take care of that today.
Heat capacity is kind of like efficiency. It’s a bang-to-buck ratio. With efficiency, the equation is output over input. With heat capacity, it’s a ratio of the heat added or removed to the temperature change. Here’s the equation:
C = Q / ΔT
This is about as hard as the math is going to get here, so just stick with me.
If we add a certain amount of heat (measured in BTUs) to a certain amount of matter (air, in our case), we’ll get a certain amount of temperature change. What this equation tells us is that the ratio of those two quantities is a measure of how much heat a substance can hold. If we get half as much temperature change for a given amount of heat added, that material has twice the heat capacity. So this quantity, heat capacity, is an important property of materials for anyone interested in energy efficiency or heating and cooling.
It’s usually easier to talk about specific heat capacity because the Q in the equation above will change with different amounts of air, the substance of interest here. By dividing the right side of the equation above by the mass of air, we get the specific heat capacity. If we rearrange a little using the magic of algebra, we get an equation you may recall from high school or college. (It shows up in introductory classes of both physics and chemistry.) Here it is:
Q = mcΔT
Look familiar? If not, hang with me just a little longer and I’ll show you an equation you may have seen before.
The next step is doing a little conversion for the mass term. When we deal with fluids, it’s usually easier to work with density, which equals mass divided by volume. So we replace the m term above with density (Greek letter rho, Ï) times volume (V). Here’s what our equation looks like now:
Q = ÏVcΔT
Whether the math is causing you to hyperventilate or not, let’s step back a second and recall where we’re going here. The original question was about how we take heating and cooling loads in BTU/hr and determine how much air flow we need in cfm. We’ve got a term in the equation now for volume and cfm is just volume over time. One of the great things about algebra is that we can divide (or multiply) both sides of an equation by the same thing. In fact, it’s encouraged!
So let’s divide both sides of the above equation by time. On the left, we end up with Q/t, which gets us to the BTU/hr we’ve been discussing. On the right, the volume, V, divided by time gives us cubic feet per minute. Of course, to end up with BTU per hour on one side and cubic feet per minute on the other, we need to throw in a factor of 60. It goes on the right side.
Also on the right side, we have Ïc, the density of air times the specific heat of air (at constant pressure, but that’s another discussion). Density and specific heat are just two numbers we can multiply, and just to be clear, we’re talking about air at sea level and near room temperature. You can’t use the equation below up high in the mountains or at temperatures far from the air you’re breathing right now. When we multiply density (0.075) by specific heat (0.24) and also by 60, we get 1.08. The final equation looks like this:
BTU/hr = 1.08 x cfm x ΔT
This is the equation I said you may have seen before. It’s taught in HVAC programs and BPI classes as well as other places. If we rearrange this equation to get air flow on the left, we end up with:
cfm = BTU/hr / (1.08 x ΔT)
And there we have it. Once we know how much heat a room needs to have supplied or removed, we can do a simple calculation to see how many cubic feet per minute of air flow we need. Of course, the cfm we need will depend on the location. You can’t just use 1.08 everywhere, as I said above. And we also need to know how much the temperature of the air changes when it goes through the furnace or air handler, the ΔT in the equations above.
Is that all?
I know what some of you are thinking now. You’re looking at all that I’ve done above and you’re saying to yourself, that’s sensible. And you’re absolutely right. The equation for cfm above is only for the sensible heat added to or removed from air. It doesn’t include the latent heat part of air conditioning, the part that deals with moisture removal.
We could go back to the beginning and go through a similar process for the latent heat removal. Heck, we could go even further back and talk about the partial derivative of enthalpy with respect to temperature. But how about I spare you those details and give you the answer right up front. Here’s the analogous equation for the total heat (sensible plus latent):
BTU/hr = (1.08 x cfm x ΔT) + (0.68 x cfm x Δwgr)
Doing a little algebra magic again, we get the equation for cooling cfm:
cfm = BTU/hr / [(1.08 x ΔT) + (0.68 x Δwgr)]
The only thing new here is the Δw variable. That represents the change in humidity ratio, and the gr subscript is for grains. Humidity ratio (often mistakenly called absolute humidity) is one of the main variables on a psychrometric chart and is measured in grains of water vapor per pound of dry air. The grain is a weird way of talking about the mass of water vapor, with one pound (mass) of air being equivalent to 7,000 grains.
When air passes over a cold air conditioning coil, two things happen. The air temperature drops and the concentration of water vapor in the air also drops as the water vapor condenses on the coil. Both of those changes are part of the cooling capacity of a piece of equipment.
BTU/hr, cfm, and the HVAC design process
What I’ve done above is to explain the relation between the amount of heat carried by air moving from one place to another and the amount of air flow required to move that heat. This is just physics. The relations come from the definition of heat capacity and the properties of air. Converting BTU/hr to cfm in the HVAC design process is a little different.
I won’t go into all the details here but after you find the room-by-room heating and cooling loads, you have to select the right piece of equipment to meet those loads. (That’s Manual S in the ACCA protocols, and you can read more about it here and here.) With heating, it’s easy. Whether you’re doing it with a furnace, heat pump, boiler, or — Heaven forfend! — electric resistance heat, you just need a piece of equipment that can supply at least as many BTUs as you need for the whole area served by that system.
With cooling, it’s a bit harder. You have both sensible and latent loads that need to be met. So you’ve got to have a piece of equipment that meets not only the total cooling load but also the sensible and latent individually. Then you’ve got to decide how much air flow you want per ton of total capacity. In a humid climate, that’s somewhere around 400 cfm/ton, plus or minus. That gives you better dehumidification from the air conditioner. In a dry climate, you might push that number up to 500 cfm/ton or even higher because it wastes energy to condense water vapor on the coil.
Then you’ve got to go into the manufacturer’s expanded data tables to select the right equipment and the right settings. The amount of heat removed by an air conditioner depends on the indoor temperature and humidity, the outdoor temperature, and air flow over the condenser and evaporator coils. The expanded data tables show you the values for certain conditions, but often the conditions you’re designing for are somewhere between numbers in the table. So you interpolate to find the numbers you need.
In the end, the piece of equipment you choose is designed to meet the heating and cooling loads at design conditions. And then it spends most of its life operating outside those conditions, in what’s called part-load. That’s because 99% of the time it’s not as hot as our summer design temperature and the other 99% of the time it’s not as cold as the winter design temperature. (The “other” there has a special meaning, of course, and I’m sure you can figure it out.)
The takeaways
If you got lost in the math up above and jumped down here, let me see if I can summarize things a bit for you. I started the article looking at the physics involved in air flow and heat. That was all based on the definition of this thing we call heat capacity, which is a measure of how much temperature change you get in a material for a given amount of heat added or removed. That resulted in the pair of equations that relate the three variables, BTU/hr, cfm, and ΔT. There’s a number (1.08) in the equation, too, and although it looks like a constant, it’s not. You have to remember to adjust it if the density of air isn’t the same as air at sea level near room temperature. (The heat capacity can vary, too, but for what we’re doing here, it’s mainly the density you have to adjust.)
Then I showed that those two equations are only for sensible heat; that is, the heat that causes temperature changes. If you have moist air (and who doesn’t want that!) and are cooling it, you also have to consider the heat involved in condensing water vapor on the air conditioner coil. That led us to the second pair of equations, which includes that heat.
But there’s physics and there’s engineering. If we had to start from first principles and do all the physics every time we design a heating and air conditioning system, we’d probably just be sitting around the fire in winter or fanning ourselves with palmetto leaves in summer. Instead, we have procedures for taking load calculation results and getting the right piece of equipment that moves the right amount of air with the right number of BTUs. The good news is that a larger number of houses get real design these days, although that number is still too small.
Now you have the answer to the original question. Yes, we know how to go from a BTU/hr heating or cooling load to the cfm of air flow needed to meet the load. The heart of it is pure physics. The design process is engineering.
Allison Bailes of Decatur, Georgia, is a speaker, writer, building science consultant, and the author of the Energy Vanguard Blog. You can follow him on Twitter at @EnergyVanguard.
Weekly Newsletter
Get building science and energy efficiency advice, plus special offers, in your inbox.













2 Comments
> "With heating, it's
> "With heating, it's easy...you just need a piece of equipment that can supply at least as many BTUs as you need.."
And distribute/mix it properly within a room and maintain proper balance between rooms (even with non-proportional room load variations).
Write an Article on Delivered System BTU
Great article as always. We encapsulate 99% of our HVAC designs in open cell foam encapsulated attics or encapsulated crawlspaces or both when 2 story homes are constructed on crawlspaces as most homes are in North Alabama. The calculation you are doing is for delivered Btu's needed. I am sure you would agree that the temperature of air that leaves the air handler is much different than the temperature of the air delivered into the room. This is especially true with HVAC systems installed in vented attics or crawlspaces. For example, the temperature of vented attics in Alabama is somewhere around 130F to 140F. When you consider a PSC air handler installed in that attic with high pressure drops due to bad duct design and installation such as undersized returns, restrictive filters, pinched and kinked flex duct, no transfers grilles in bedrooms, etc. you are not getting the proper cfm out of the system and you are not getting the proper btu delivery. On Wrightsoft HVAC design software you can easily compare the heating and cooling load for ducts located in a vented attic vs an encapsulated attic, ducts in a vented crawlspace vs an encapsulated crawlspace and so on. The best comparison I have found is that for a one story home built on a crawlspace and showing the difference in heating and cooling loads in a vented attic vs an encapsulated crawlspace. We also require variable speed air handlers in all of our homes we design and insulate. We start out with a 0.8 available static pressure and we limit pressure drops as well as total effective length of the duct system. We then don't worry much about duct leakage, duct insulation (though some is necessary in our area to prevent condensation), and air velocity.
Log in or create an account to post a comment.
Sign up Log in