A Consumer Friendly Home Rating System
I’ve finally found my dream house rating system, which is just like an EPA rating label for an appliance or a car:
I’ve been saying for years that as consumers get more educated about energy efficiency in homes, the demand for efficient homes will increase, and the selling price of those homes will increase.
Well, I’m tired of waiting*, so this rating system gives the consumers what they need to know NOW.
NOTE: this is a rating system, and by definition, can only be measured on a house that has been built. This will prevent the most insidious types of greenwashing, like advertising a LEED rating before the home has been built.
There isn’t any “embodied energy” rating here, but I think a third scale for that would start making this rating system too confusing. The embodied energy of a low energy new home is small enough to be ignored for now. If and when a carbon tax is implemented, that will be reflected in the selling price of the house.
*I realized that until Realtors understand this stuff, most consumers have no hope. I haven’t yet met a Realtor who really understands the difference between a KW and a KWH.
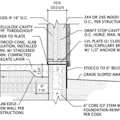
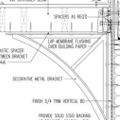
GBA Detail Library
A collection of one thousand construction details organized by climate and house part







Replies
As long as we continue to identify as "consumers" - instead of citizens or people or, better yet, one node in the vast and interconnected Web-of-Life - we will never have any hope of achieving a sustainable cultural paradigm, and home energy ratings will be little more than another sales gimmick.
I found this on DemocraticUndergound.com:
When did we become consumers instead of citizens?
Around the time corporations got citizen status, I would guess.
What a terrible word -- consumer. Makes you think of a voracious gluttonous eating shark machinery devouring whatever is available. One large mouth moving along, like a Pac Man. Eat up the bullsh-t, pig out on instant gratifications and get fat headed and lazy while the corp/gov/media machinery makes us believe this is what freedom and democracy is - all about credit cards and designer labels and diet fads and whose zooming who in hollywood.
Yes, 'they' surely hated us for our freedom when we were once citizens.
In terms of a simple energy rating system, we already have the national HERS program, as well as the new DOE Home Energy Score. While the Oregon Energy Performance Score offers the addition of a carbon rating, I'm not sure why we need a dozen competing score cards. Let the DOE, which has national cred and the resources to propagate a standard, take the lead on this.
The DOE scoring system isn't as simple as this system, which mimics the EPA ratings we have lived with for over 30 years. So yes, let's have one system, just let it be easy to understand.
The DOE Home Energy Score is just like an appliance rating label. It show where a particular house is on a simple scale from fair to best (1 to 10), rather than using an absolute energy consumption scale in MMBTU which no layperson understands.
Kevin great posting. I am very interested in all of this and having free access to rating software that is easy to use, accurate and easy to understand. Great post. You may never get some here to ever do anything but argue a counterpoint no matter what point you try to make. Such as it is here at GBA.
The DOE system is simple, but it's not simple enough.
The dollars per year figure is the only number that the lay person will understand within 5 seconds. DOE is not showing that, and that's what I want. That's what I get with the EPA appliance label. The absolute MMBTU consumption is important to a wonk like me, and I'm glad it's there, but the homebuyer doesn't care.
Since energy costs vary from region to region and from year to year, an energy cost rating does not allow comparisons across regions or time.
For the same reason, EPA automobile ratings show MPG and not $/year.
A truly comparative rating system has to be on a unit-less scale, such as the DOE system uses.
@ Robert
> EPA automobile ratings show MPG and not $/year
That's not exactly correct, Robert. The stickers adopted a couple of years ago show expected cost/yr.
http://www.fueleconomy.gov/feg/ratingsNewSticker.shtml
Best wishes,
Joe
With the volatility of gasoline prices, that's pretty silly.
But what would I know. I've never bought a new car.
Oh, I think the analogy is a pretty good one. Consuimers, who don't know much engineering (mechanical or construction) and who don't really care about it anyway, do understand $$$. Even if it's not to the penny, or the dollar, it's a graphic demonstration of a "difference" between two complex systems.
Any time you go to a dimensionless scale, then you have to start explaining things. Dollars don't need explanation. The homebuyer isn't comparing year to year or region to region, only house to house within the same year and region.
The total consumption number in the EPS, which also has dollar amounts on it, is much more straight forward to consumers than the 1-10 scale provided by the DOE Home Energy Score. What is a 1? What is a 10? And how do I change? It is actually not a true comparison across housing stock because it is a statistical scale. Your home is placed on the scale with reference to other homes of similar size within your region. A code home will score very high on the scale, and an Energy Star home will most likely score a 9 or 10. So when we are pushing people to build more efficient homes where does the Home Energy Score allow them to go? Everything better than code is lumped together at the top of the scale, whether it's slightly better than code or net zero. The EPS provides the granularity to distinguish between these homes, which is much needed when trying to bolster high performance building efforts.
Another thing I would advocate for is that this rating isn't issued until the house has been lived in for a year with simple data collection during that time. Insulation inspections and a HERS score from a good rater can tell most of the story, but not all of it. Only actual results can be trusted 100%. (The usage of a single house with its unique family can be normalized to be comparable to a standard. Statisticians do this all the time.)
Once the builder has some history of consistent scores, then he could be "approved" to rate a house before it's built.