Thermal Bridging with PVC vs. Z Flashing
I recently toured a where the designers noted the use of PVC rather than metal z-flashing at the bottom of wall/sill area to reduce thermal bridging. How important is this likely to be in a wall 2″ external foam (above and below ground) and 2×6 wall construction (CZ6)? Is there a simple calculation to model this? It total, a rather large area that is affected, and if attached to the sill plate, a rather direct bridge to the interior.
Here’s one source for the flashing:
https://plasticomponents.com/product/heavy-duty-z-flashing/ — I worry it might be hard to source non-metal flashing.
GBA Detail Library
A collection of one thousand construction details organized by climate and house part
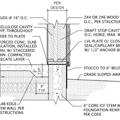
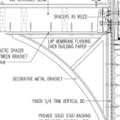







Replies
Thermal bridging in a piece of metal flashing is going to be minuscule in the scheme of things. The conduction is a factor of the sectional area of the flashing. So you're talking about a tiny fraction of an inch of thickness of material compared to the total wall surface area. I would challenge anyone justifying their choice of PVC on a thermal bridging excuse to support their assertion with calculations or tests.
Personally, whenever there is a reasonably economical alternative to PVC (and there almost always is) I go with the alternative. PVC has a lot of cheerleaders. But the bald fact is that its production and disposal cause major environmental problems.
As far as the calculation, it would be the same as how we calculate the average insulation value of a stud wall with insulation between studs. It's a factor of the areas of the 2 materials (studs and insulation) and their respective R-values.
Rstud*PERCENTstudarea + Rinsul*PERCENTinsularea = Average insulation over total wall area
We'll try that with metal instead of a wood stud. We'll do a wall segment 1' wide by 8' high, with 18 gauge sheet metal flashing (1/20" thick).
Total Area = 8 s.f.
Metal thickness in feet = 1/12/20 = 0.004167 ft.
Metal Area for 1 foot of 8' high wall = 0.004167 ft * 1 ft = 0.004167 s.f.
Metal Area as a percent of total wall surface = 0.004167 / 8 = 0.05%
Insulation Area = 8 ft - 0.004167 ft = 7.99583 s.f.
Insulation Area as a percent of total wall surface = 7.99583 / 8 = 99.95 %
Metal R value = We'll call it zero for a worst case.
2" foam Insulation R value = 10
drumroll please!
0* 0.05 + 10*99.95 = 9.995 average R value
So, as you can see, the effect of the metal flashing is negligible.
I have masters degrees in both architecture and structural engineering. In other words I'm a "numbers guy". But I'm not perfect. If I've made a mistake someone is sure to point it out. That said, I think you need to challenge the architects to refute my calculation. If their answer is that it doesn't apply to "real world" situations, then they need to justify their claims with results from tests on real world, full size assemblies.
I wouldn't worry about the thermal bridge of a few pieces of flashing, but sure would if using metal studs: " Put an R-19 batt in a steel stud wall and you are lucky to get R-5 to R-6 in the real world." https://www.buildingscience.com/documents/insights/bsi-005-a-bridge-too-far
Antonio,
Your analysis is flawed due to the simplification of heat flow in a 2-D model. The flanges on the flashing have a significant impact on the total R-value that requires 3-D analysis to calculate. Essentially, the flanges act as radiant and convective heat sources/sinks. In your 2-D analysis, even if the flashing was a superconductor, the effect on R-value would be the same. Instead in that scenario, the interior flashing flange temperature would be the same as the exterior flange temperature and its effect on wall R-value would be calculated based on the surface area of the flange, not the cross-sectional area of the flashing itself. I have witnessed this effect on copper pan flashings that went across the entire wall thickness so that they were exposed to the interior and exterior environment. The inside flange of the flashing was well below freezing in wintertime and developed a thick (about 1/8" or more) coating of ice over the 3/4" height of the flashing. That certainly has a nonzero effect on the overall R-value of the wall. The same effect happens with aluminum window frames that have no thermal breaks.
A better approximation of the effect of the metal flashing would use the surface area of the flange in place of the cross-sectional area of the flashing. Using your above numbers with a 3" vertical flange, the total area of flashing jumps to 3%, and the average R-value decreases from 9.995 to 9.7. Still a small effect, but not quite as small. For me, the use of nonconductive flashing is more to avoid the condensation issues than for energy savings. I agree that PVC is not the best choice environmentally and would love to see a different corrosion resistant low-conductivity material. FWIW, the conductivity of stainless steel is 20x lower than copper and is similarly priced, but a bit more difficult to work with. PVC is about 75x less than copper.
Thank you, Peter. That all makes total sense.
In the original comment the poster also referred to 2" of external foam. I assume that's not the total insulation for the wall, but just exterior rigid insulation supplementing insulation between studs. I guess, to get the full picture, we'd need to consider all that stuff inboard of the rigid foam as well.
Many thanks for the informative discussion
Antonio - the wall is designed as 6" studs, filled with blown cellulose or fiberglass, sheathing/WRB, then 2" external foam. The flashing would extend under the foam to the external sheathing.
To complicate the analysis: the flashing is likely to be attached to the wall at the sill plate, so it's effectively in contact with what is already a thermal bridge - i.e., in cold weather the effective insulation at the sill is going to be 5 1/2" of wood for the sill, with the sheathing and drywall, so maybe R 12 versus in the cavities @ R21 or so for the blown insulation. I was wondering what the impact is once you multiply the small cross-section of the flashing by the entire length of the perimeter of the house. I think the discussion above provides the info I was looking for - thanks again.
If you want to use metal and minimize thermal bridging, and cost is not an issue, use stainless steel. The thermal conductivity difference between stainless and mild steel (let alone copper or aluminum) is mind-boggling.