
Image Credit: Allison Bailes
If your attic is going to have 50 bags of insulation blown into it, does it make much of a difference if it goes in flat or lumpy?
One reason that I’m interested in the question is that my dissertation in grad school was called “Flat or Lumpy.” (Of course, it had the requisite incomprehensibility in the subtitle, with words like “heteroepitaxy.”) Those two words in the title, which cut to the heart of what my surface physics research was all about, also describe a property of insulation that’s important in building science.
Lumpy attic insulation = poor average R-value
Let’s look at an example. If the insulation goes in perfectly flat, let’s say we have a nice uniform R-value of 30 throughout the attic. (We’re going to ignore the complicating factor of the framing and assume it’s a continuous layer of blown insulation.)
There are all kinds of ways it can go in lumpy, but let’s assume that 50% of the attic has lumps of R-50 insulation, and the other 50% is valleys with only R-10. We want to find the average R-value of this lumpy configuration. It’s the same amount of insulation, and the average of R-50 and R-10 is R-30. But, how does it really perform?
Let’s do the math!
Warning: This section contains mathematics. If you feel nausea or dizziness, skip to the conclusion below. If you feel excited by this discussion, see your local physics department. If your arousal lasts longer than 4 hours, you should work through the problems in Classical Electrodynamics by J.D. Jackson.
Now, we can’t just average the R-values. If we did that here, we’d get R-30, and we’d be wrong. Heat will take the path of least resistance, and the less resistance you give it, the more heat will flow. If you’ve studied physics, engineering, or building science, you’ve probably seen the equation for heat flow by conduction: Q = UA ΔT = 1/R ∙ A ΔT
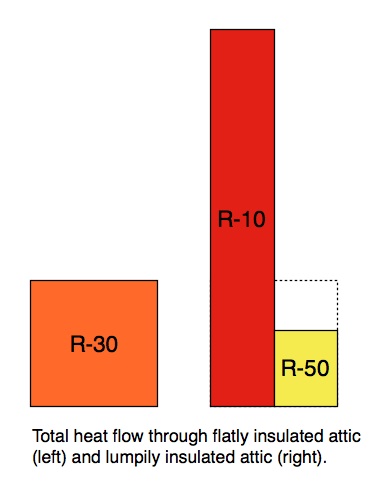
If we calculated the amount of heat flowing through the lumps and valleys in this attic, we’d see that the R-10 half (the red bar below) would allow way more heat to flow than the R-50 half (the yellow bar below). In fact, the R-10 valleys, having one-third the R-value, would allow 3 times more heat to flow than if it had R-30. The R-50 lumps would allow only 3/5 the heat flow as R-30.
Also, the total amount of heat flow is greater for the lumpy insulation than for the flat insulation. As you can see below, the red and yellow parts together add up to a lot more heat flow than the orange — actually 1.8 times as much.
Because the lumpy insulation allows more heat flow, it’s got to have a worse average R-value. Clearly, the average R-value is going to be more influenced by the underinsulated part than by the overinsulated part.
To find the average R-value the correct way, we first have to convert R-values to U-factors. R stands for resistance, as in resistance to heat flow, so the higher the number the better when we’re talking about building materials. U-factor, the heat transfer coefficient, is the reciprocal of the R-value, so the lower the number, the better. (For a better understanding, see this Wikipedia article about R-value and U-factor.)
The equation for average U-factor is:
Taking the attic as 1,000 square feet total and putting in 1/R for U, we get:
Taking the reciprocal of 0.06, we get the average R-value of about 17, which is much lower than the R-30 we’d get by incorrectly averaging the R-values.
Get out your rake
As I said above, heat takes the path of least resistance, so the amount of extra heat going through the R-10 half far exceeds the extra heat flow that’s stopped on the R-50 side. Instead of getting an R-30 average, the lumpy attic has an R-17 average.
In practical terms, this means that if you see an attic with lumpy insulation, get in there with a rake and smooth it out. In the example I just worked out, you’d nearly double the R-value without adding any extra insulation!
Another common example of the flat-or-lumpy conundrum is an attic that’s perfectly insulated except for one small area, say the pull-down attic stairs. We can go through the same steps as above and show that an attic that has a uniform R-30 over 99% of the area and 1% at R-1 (the pull-down stairs) will have an average R-value of 23.
That’s right, those pull-down stairs can decrease your overall R-value by 25%. One small uninsulated area reduces the R-value dramatically.
In my graduate research, getting smooth, flat layers was our goal. In the building science of insulation, flat also wins out over lumpy.
Allison Bailes of Decatur, Georgia, is a RESNET-accredited energy consultant and trainer. He is also the author of the excellent Energy Vanguard blog. For a GBA review of Bailes’ blog, click here.
Weekly Newsletter
Get building science and energy efficiency advice, plus special offers, in your inbox.





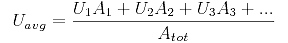
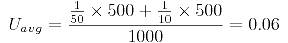










31 Comments
Nice post, Allison
While not perfectly analogous due to solar effects, this type of analysis should be essential when considering additional glazing on an otherwise high-R wall.
P.S. Thanks for the mention of Jackson. I still have his book, but I don't keep it with the rest of my textbooks. It's on a shelf with some copies of religious texts... fear of electrodynamics is the beginning of wisdom.
icons
Great point, Ben. The ratio of glazing to wall area has a huge effect on a whole wall R-value (including glazing) for the same reason that flat insulation is better than lumpy. Here in Georgia, it would be R-3 windows versus R-13 insulated wall cavities, and once you know the areas, you can do the math.
ENERGY STAR Version 3 is on the right path, though, by addressing thermal bridging. It doesn't set any kind of threshold for whole wall R-values, including the glazing...yet. I hope that'll be in a future version.
On a shelf with religious texts is exactly where Jackson's book belongs. It's definitely achieved icon status.
Glazing that neither gains nor loses E
Ben, This last year I have read about higher R windows having no net gain or loss of E. Selecting the right windows for each wall of a house along with placing overhangs, porches, trees is more important. To me that means we can stop thinking about windows as places where lower R has any negative impact. I know it's not that simplistic, but I like a rule of thumb like that which follows my gut instincts.
Glazing that neither gains nor loses E. Not quite the same as lumpy insulation though, with poor design it could be.
Another thought I have had every winter. My home has a huge portion of it facing south being heated by solar gain (salt box roof with black shingles.) Temp readings on cold sunny days go above indoor temps when I take readings like I did today. My gut says the insulation is meaningless for the sunny hours of winter days. Which then still points me to air leaks being the main aspect of saving E worth attacking as we work to lower our E useage.
I like this blog post, Thank you Allison
No net gain or loss of E?
aj builder, I'm not sure what you mean by 'higher R windows having no net gain or loss of E.' It makes a bit more sense to me if you reverse the R and E, and if by E, you mean e, the emissivity. In a cold climate, you want windows with as low a U-value (high R-value) as you can get and a high solar heat gain coefficient (SHGC) if they can catch any sunlight to help heat the house.
No religious texts thank you
Allison you posted while I did, I hope you understand my point about windows having no net effect in northern climates anyway, since the study I read was done in Canada as I remember.
Real homes built that are not mathematical models have real E gain as well as E losses. For my climate my interest is in not having losses. It made my day to see that the study claims I can put in windows that seem to me if designed right will have NO effect such as that your math is not needed to be calculated and accounted for. No?
Good Stuff
Allison,
These weaknesses are very interesting
There is an illustration of "Cold Edge Effect" in Bill Rose's Water Book
Showing how a sudden change of R-value can result in a "Cold Edge" that is much colder than the predicted temperature at the weakest link.
0 adds or subtracts 0
Allison, the study in Canada stated that correctly chosen windows would not effect energy (E) in a negative way in a northern climate.
My point is, if I chose my windows as per the Canadian study, that doing the math of U value is not needed and is a waste of time and effort and misleading one who has a goal to use less E. per given design encompassing X% of window to wall.
Martin Holladay, https://www.greenbuildingadvisor.com/book/export/html/15600
I know basic math. 0 added into an equation of such will change the result by 0. No? I say yes.
Back to the blog topic Allison. Very interesting blog. I started playing U value addition/subtraction math this last summer due to someone else bringing up the effects of small areas of poor R value having large effects on whole assemblies. Great topic, hope it is explored more and often. Again Thanks for putting up the post.
Attic Storage Area
Great article Allison and thanks for the equations. In just about every house we go in, there is plywood installed on top of the ceiling joists compressing the insulation and limiting it to about 6" or 8" in a decent portion of the attic. Homeowners want their storage and do not want to pay to remove the decking, furr up the ceiling joists, add insulation and reinstall decking to get a proper insulation job. Now we can show them exactly how much it is hurting them. Have always wondered if it did any good to just add insulation in all other areas or not - typically have resorted to just air sealing in these circumstances knowing they do not want to spend the extra money to do it right.
Thanks again - one of the more helpful blogs I have seen in a while.
Gonna hafta check out Rose's book
John, thanks for the tip. I'll have to get my hands on a copy of Bill Rose's book and check out the 'cold edge' you're talking about.
Other options for decked attic floors
Danny, decking on the floor of an attic that limits insulation to what you can get into a 2x6 or 2x8 cavity has the same result as the lumpy insulation I discussed in the article, as you've surmised. An alternative to pulling up the decking is to move the building envelope to the roofline and creating a conditioned attic. If they want to use the attic for storage, that would be a better option anyway. Martin just wrote about this last week.
Conditioned attic as a solution
Yes, we do present that as on option but has its fair share of drawbacks and typically even more expensive than removing the decking (to do it right anyway). Most homes around here have an 80% furnace in their attic too, creating a few more issues/expenses to deal with.
We have seen some moisture issues with drastically changing the thermal envelope of the home too, so not a huge fan on foam on existing homes, especially an older home with plaster ceilings. You can see a discussion we had on this last summer here:
https://www.greenbuildingadvisor.com/community/forum/general-questions/17488/high-humidity-issues-spray-foam-attic
50 bags ... flat or lumpy ... or perhaps wavey
If limited to 50 bags and a "rake"
would it not be better to pile a lttle more above each joist
and leave a little less in the joist space?
Response to John Brooks
John,
Good luck with that!
You'll be like a Zen monk with his rake, doing attic meditation for hours, trying to achieve perfect furrows ...
Allison, Ben what are you two learning
Hey guys, any comments as to what Robert and I are saying?
Have you rethought how windows effect whole wall R?
So much of building homes is counter intuitive when not seeing the whole environment.
That's why I mentioned a short list of very important environmental items earlier.. location, location, location of all (Windows, sun, trees) much more informative for window energy design factors verses doing wall/window U math.
Your thoughts gents?
I must be missing something.
Robert and AJ,
I have always considered the thermal effects of glazing in a two-step process. First, I would average the U-factors of a given wall construction (windows included). Second, I would include solar heat gain from windows as an average seasonal heat source (affected individually by orientation, shading, etc). In other words, I have always split window effects into two separate categories: thermal resistance (U-factor) and solar gain (SHGC and site-specific characteristics).
Is it more accurate to consider windows and their surrounding walls as two independent features? Should I calculate a wall's U-factor while ignoring its windows, and then add windows in as independent energy sources/sinks?
My assumption is that these are two paths to the same result. Am I missing something?
Google translate?
AJ,
Slow down your typing speed, man.
Please translate: "location, location, location of all (Windows, sun, trees) much more informative for window energy design factors verses doing wall/window U math."
translation
Trees and porches and their locations are the important factors among a few others as Robert details.
Ben, yes there are two ways to the same end result. But, if you take my less travelled road you find that it opens up huge enlightening options to one's design/purpose/goals/wants/needs/function/fengshui....
And it is simpler and yet one can then think, Windows windows Windows. Who doesn't love windows?!?
design freedom
AJ, I think what you're saying has a lot of value. Your design strategy, if I'm not misunderstanding, is to first calculate the U and SHGC values that result in no net energy loss for your location. However, the opaque wall will have a net energy loss. So, you still have to take into account the window-to-wall ratio in order to get an accurate prediction of energy use requirements. Is this accuracy necessary? Maybe not. If the wall is insulated well enough, you would have the design freedom to locate and size windows however you want on a given facade.
I'm not sure it's possible to have north-facing windows in the Northern Hemisphere that are energy neutral, however. That means you do have to calculate the U values for those windows and walls, using the average U-value formula Allison described.
Questions about the cotton candy insulation . . .
Is this stuff loose fill fiberglass? What is causing it to stand up like that?
I've never blown anything but cellulose, and it's been fairly easy to get a fairly uniform layer.
In the photograph, is this problem something that is common to that type of insulation, or just an example of a poor installation?
Thanks
How we measure affects how we think
Good article. It's unfortunate that we seem to be stuck with using R-value as a measure of building components, when U-value, being directly proportional to all of the things we really care about (heat loss, dollars, environmental impact) is a much more intuitively accurate measure. Part of the problem with U-values is that they're (hopefully, at least) fractions less than 1, so you get things that look like "0.31", for example, which is a hard number for most people to wrap their heads around.
What I like to do, especially when talking to lay people, is use U-value x 100. This gives you a nice integer that you can think of as being a relative measure of either dollars on your utility bill, or gallons of heating oil, or pounds of CO2--as you choose. By this measure, a square foot of well-insulated attic might be a 2 or 3, a two-by-six wall might be a 5, a replacement window might be a 30, and a single-pane window around 100. Air leakage is another matter, of course.
PS: Similarly, I think we'd do better to think of vehicle fuel efficiency in gallons per 100 miles, rather than MPG....
Response to Steve Paisley
Steve,
Assuming you accept the usual equations, namely
U = 1 / R and
R = 1 / U ,
I can't understand your reasoning. In what way is U-factor a "much more intuitively accurate" measure than R-value ?
Response to Daniel Ernst
Daniel, the photo at the top of the page is indeed blown fiberglass. When first blown into the attic, it was probably nice and smooth, but this particular attic had a serious critter problem (squirrels), and within a few months, they'd tunneled through much of the insulation, leaving the lumps you see above. Squirrels can make a mess of cellulose, too.
lumpy attic insulation
Mr Bailes analysis assumes a uniform "heated area" temperature. Often people close off certain rooms to intentionally keep them cooler (bedroom). In that case placing thicker insulation above the warmer rooms is both well advised and tharmally more efficient. I do this myself - preferring a warm bathroom (72F) and quite cool bedroom (64F) upstairs.
small correction, lumps and valleys
It's little more than a typo, but imagining that this useful article might be reproduced or quoted widely, I think it would be worth correcting a reversal of the lumps and valleys vs. R-Values in the third paragraph of the "Let's Do the Math" section. Here is the problem, in the second and third sentences of the following text:
"If we calculated the amount of heat flowing through the lumps and valleys in this attic, we'd see that the R-10 half (the red bar below) would allow way more heat to flow than the R-50 half (the yellow bar below). In fact, the R-10 lumps, having one-third the R-value, would allow 3 times more heat to flow than if it had R-30. The R-50 valleys would allow only 3/5 the heat flow as R-30."
Would you not agree that R-50 would arise from greater insulation thickness, hence "lumps", while R-10 exists in the thinner insulation "valleys"?
Editor's response to Derek Roff
Derek Roff,
Thanks for catching the error! I've made your suggested correction.
Insulating over garage
This is very interesting. It never occured to me that not insulating over "dead" space, e.g. garage, porch would affect the R value of the rest of the house. Our builder never gave us an option. We have 3 covered porches that have no insulation as well as our 3 car garages which have planks of plywood over the rafters for storage but no insulation. Does this then affect the rest of the house.
Another question. We found out after we moved in, that our insulation was at best R-19. After several years of calling, the insulation company came back and blew in cellulose (I assume since it's gray) over Certainteed fiberglass. Any problems with that?
Response to Anonymous
The analysis above doesn't apply to the lack of insulation over garages and porches. It applies only to surfaces where the temperature difference is the same. Garages and porches generally don't have the same temperature as the conditioned space in the house.
No, it's perfectly OK to add new insulation on top of old. Cellulose will do a better job of resisting air leakage, too.
Followup
I have cellulose in my attic, and want to add more to meet the requirements of my part of the country. SInce a rake won't get everything "Lump Free," would it be better to roll out fiberglass insulation on top of the cellulose? To Bad you can't use an electric mixer like mashed potatoes :-)
Lumpy or Bumpy
When I saw the title of this blog, I was wondering what kind of blowing machine would eject lumps of fibrous insulation, but then realized you meant "bumpy" or irregular surface, not lumps of varying material density. Clarity of terms is important.
It's a poor testimony to the working knowledge of the design and building trades that it should require a PhD to educate us about the importance of averaging U-factors. This should be thermal design 101 and in the toolbox of every building professional. I teach these basic formulas - as well as the paradoxes they seem to present - to all of my students (and have shared this information in forum discussions).
What AJ is trying to say in his usual clumsy way, and what Ben Wilson apparently doesn't understand, is that the percentage of glazing in a wall is not at all analogous to bumpy insulation. Insulation has one primary function: to resist conductive heat loss (or gain). Windows have multiple functions, including aesthetics, views, daylighting, ventilation and solar gain (for cold climates). Thus U-factor (or R-value) can not be the determining characteristic, particularly given that even a modestly insulating window can offer a net energy gain over the course of a heating season, if properly oriented and balanced with thermal mass. Almost any glazing of R-2 or better can provide a net energy gain in the right climate with sufficient solar availability, so the effect on average wall U-value is not analogous to lumpy insulation.
However, the effect of varying insulation thickness or of insulation voids and thermal bridges can be dramatic and their relative effect increases with installed R-value. This is also an unacknowledged problem with spray foams which typically get installed in a non-uniform layer.
No Rolls
Chris,
It would be far better to add more cellulose.
AJ Speak for Yourself
I am in no way saying the same thing as you are about windows, and you do not have my permission to use my name to justify your nonsense.
U-values of all envelope elements must be area averaged to determine maximum design heat loss/heat load for the building in order to properly size the heating system. The heating system has to be able to keep up with nighttime heat loss when the sun don't shine.
Properly oriented windows of the appropriate SHGC and U-factor can reduce the annual heat load, depending on local solar availability and site shading coefficients, but the efficiency of a thermal envelope is dependent on the average U-factor, infiltration rates, and radiant losses or gains.
While it's true that good passive solar design can reduce the net heat load of a building, it does so at the expense of thermal envelope efficiency. It's a balancing act that cannot be optimized except by doing the math.
Log in or create an account to post a comment.
Sign up Log in