Author’s Note, June 21 2019: I’d like to leave this story as is for the time being, even though–as my wife is wont to point out–I only got the story about half right. So, please read on but ONLY if you include the comments, certainly those of the ever-wise and kind (particularly to the author), Bill Rose.
This is a story. Much of this story I believe to be true, but I can’t document much of it either. It all just makes sense, particularly as parts are conveyed by Bill Rose, our industry’s heralded building-science historian (see #2 in Bill’s to-do list for the building industry). Some of the story is based on one or more conversations I have had with Bill, which usually started something like this:
“Bill, where the hell do the units 1 grain of water and 1 inch of mercury vapor pressure come from in our unit of measure for water vapor permeance?”
Of the four units of measure in the perm, two are familiar and reasonable—1 sq. ft. and 1 hour (OK, let’s ignore the fact that the entire rest of the world thinks—and rightly so—that the foot, and therefore the square foot, is nuts as a unit of measure). The other two—1 grain of water and 1 in. of mercury—are just plain bizarre.
What’s a grain of water?
A grain of water is 1/7000 of a pound of water. Yes, there are 7000 grains of water in one pound of water. There, that’s helpful, right? What about this: With a very fine dropper, such as this micropipette, one drop of water is equal to about 1 grain of water (see the image below).

Well, that makes more sense, using a liquid or volume measure for water instead of weight. But that’s not what we use. Why weight and why grains instead?
Agriculture cares about grains of water, particularly in terms of grain elevators and the moisture content of the grains stored in them. The water content of grains affects their weight and size. It affects dust and fire safety. And when grains get too wet, water content can lead to degradation.
And here is a key to the story of how we arrived at the perm: It was wood scientists at the Forest Products Lab who first cared about how vapor moves through building materials. Why? Because paint peeling off of clapboards on walls that were insulated turned out to be caused by vapor and condensation (See this GBA blog by Alison Bailes).
Well, the Forest Products Lab is part of the Department of Agriculture. I can just imagine one of their building geeks chatting over the water cooler with an agriculture science buddy about really small units of measure for water. Believe it or not, we are pretty sure that is why we use grains of water. The Forest Products Lab needed a small unit to work with and their agriculture colleagues obliged.
Author’s Note, June 21 2019: The paragraph above is flat out wrong and quite embarrassing. Not just because I got the story completely wrong here, but more importantly because I confused a fictitious counting convention–a number of irregular particles per pound–with a true unit of measure, the grain.
“grain – 5. the smallest unit of weight, in most systems, originally from the weight of one plump grain of wheat. In the U.S. and British systems, as in avoirdupois, troy, and apothecaries’ weights, the grain is identical. In an avoirdupois ounce there are 437.5 grains; in the troy and apothecaries’ ounces there are 480 grains (one grain equals 0.0648 gram).” From Random House Unabridged Dictionary, 2nd Edition.
Okay, so what’s one inch of mercury?
There are a slew of units to choose from for vapor pressure including atmospheres, pascals, and pounds per square inch (PSI). But how much vapor pressure is 1 in. of mercury?
Let’s go to the amazingly friendly psychrometric chart so we can see the air temperatures and relative humidities that correspond to a 1 in. of mercury water vapor pressure difference (see the image below).
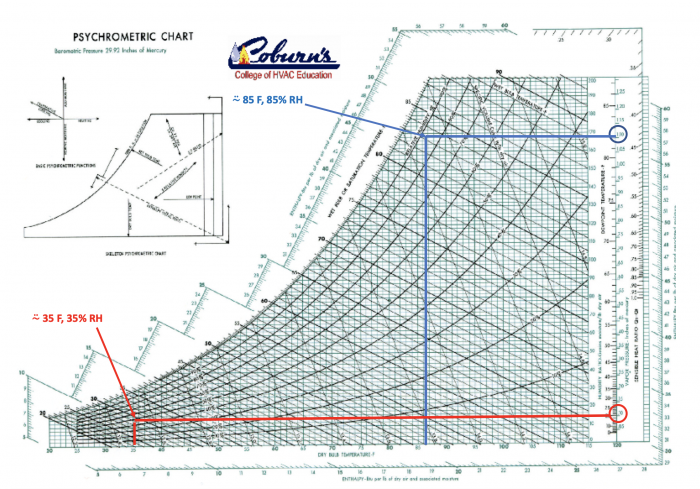
The blue circle in the upper right calls out 1.10 in. of mercury water-vapor pressure. You can follow the blue horizontal line to the left to reach about 85% relative humidity and then down to 85°F. That is roughly hygrothermal conditions inside a hothouse for growing tomatoes.
The red circle on the lower right calls out 0.10 in. of mercury water-vapor pressure. You can follow the red horizontal line to the left to reach roughly 35% relative humidity and then down the vertical red line to 35°F. That’s about the hygrothermal conditions inside a typical refrigerator.
So a vapor pressure difference of 1 in. of mercury is not common or representative in building environments at all. And typically in building science we use pascals to measure pressure. So why, in the case of perms, are we concerned with inches of mercury?
It’s all driven by the common numeric
Yup, it’s all about the “ones.” Bill told me (and I am paraphrasing): “I’m pretty sure they chose the units so that everything was a “one” and the perm represented a rate of vapor transmission that they thought retarded vapor movement enough to control wintertime interstitial condensation for certain walls in cold climates.”
So, perms are screwy units. But what a great story we get to tell. I mean, all those poor building scientists from the rest of world having to hail “nanograms H2O per square meter per second at 1 pascal” (1 perm = 1 gr / (ft2 × hr × in Hg) = 57.4 ng / (m2 × s × Pa). Sure, it’s way less archaic, but is there as good a story behind the units?
____________________________________________________________________
Peter Yost is founder of Building-Wright, a consulting company in Brattleboro, Vermont.
Weekly Newsletter
Get building science and energy efficiency advice, plus special offers, in your inbox.














18 Comments
Great Article !
Peter,
I'm writing from an airport so this comment will be short and missing references. Thanks for choosing to cover the story.
A "grain" is an avoirdupois measure of weight. I'm headed to France, and that word translates as "to have weight", except there should be a "d" before the "s", so it actually reads "to have peas". These measures were used by jewelers and others who dealt in small weights. The English/us/imperial system has measures of weight but effectively lacks a measure of mass. Mass is fundamental; weight is mass dependent on gravity and buoyancy. A grain is about the size of a drop, maybe a big drop, or water.
There was a building science conference in 1948 where this matter was discussed, and where they intended to nail in place the requirement for a vapor barrier, introduced 6 years earlier. Three researchers participated among many other participants. Ralph Britton had introduced the vapor barrier in a document he wrote for the Housing and Home Finance Agency. Frank Rowley from the University of Minnesota had studied walls and attics in doghouses built within a cold climate chamber. Elmer Queer from Penn State was the prime theoretician. At the end of the meeting they sought to put a name on the unit of permeance they'd all been talking about, to be in the class with newton, watt, pascal,... They nominated the names a britton, a rowley or a queer, but adjourned before a name was selected. Not sure when they actually selected the term "perm".
Bye for now.
My wife, who is with me in the airport, corrected me. The spelling avoirdupois did mean to have weight in old French--the "d" was added a century or two ago. In French "avoir du poids" usually means to have substance, to be able to influence decisions. In 1959, the avoirdupois system was formalized, in which an avoirdupois pound was considered a unit of mass, not weight. Au revoir.
You do learn something every day. It turns out there is a metric perm which closely matches the US perm: 1 gram of water vapor per day, per square metre, per millimeter of mercury. There is no SI unit, though, so it's defined as nanograms per second per square meter per pascal.
There are a couple of questions for the next trivia night!
Not only can you learn something everyday, sometimes you can also learn from the comments.
I'd rather have the peas, if it's all the same to you. À chacun son goût
and for those of us who might need a review of the difference between mass and weight: Kahn Academy has a great 10 minute unit on this topic:
https://www.khanacademy.org/science/physics/centripetal-force-and-gravitation/gravity-newtonian/v/mass-and-weight-clarification
Peter
Sal Khan's explanation is oversimplified. Using the distance of from the center to the surface of the earth (as he did) models the mass of the earth as a point mass one earth-radius away. But the real mass of the earth is distributed, not a point, so the direction of some of that gravitational pull is distributed away from the center, and the gravitational force experienced at the surface by the smaller mass is not identical to that of the earth's mass concentrated at a point in the center. (But a video calculating the error would take longer than 10 minutes. :-) )
I think you will find that the sum of all those gravity vectors averages out to the centre of mass.
In direction but not in magnitude. For an extreme example, there is little net gravitational force as you approach the center of the earth. The opposite would be true with a point mass. As Dana says, distributed mass doesn't have the same effect as a point source.
I'm not sure what your point is. What I'm saying is that when you account for all the gravity vectors of the distributed mass, it still ends up to have the same effect as the total mass being right at the centre of mass.
That's right. The vector sums of gravitation the sectional discs have the same direction pointing toward the center, but not the same amplitude as the equivalent masses of those discs /rings concentrated at the center. That's one of the easier ways to model it mathematically, but even that isn't very precise. How many digits of accuracy are we looking for?
To make it even more fun, the earth isn't precisely spherical, and the centrifugal forces on a spinning quasi-sphere changes the weight of an object at the surface measurably by location.
Or, maybe we can just call it a point mass and say, " It's good 'nuff for the kind o' girlz I go with!" :-)
It's perhaps a bit silly to think too precisely about it in armchair discussions of these things, but sometimes better precision really matters. About a dozen years ago I designed some beam deflection & imaging electronics for an extremely precise ion microscope. The earth's rotation during the flight time from the ion gun to the target mattered for rendering the image accurately. The rotational displacement varies with latitude, and the flight time varies with accelerating voltage at the ion gun. (The total flight path of the ion was only a couple meters, but ion velocities aren't the speed of light.) Ignoring the effects of latitude, earth rotation & ion velocity when processing the image created distortions big enough to matter, given the intended precision of the instrument. (At max resolution it is possible to discern & measure relative locations of individual atoms in a crystal lattice with those microscopes. It's pretty kewl stuff- too bad I wasn't the one who thought it up! ;-) )
I don't see how it matters if the amplitude of the areas matches equivalent masses concentrated at the center. If you examine the gravitational force exerted by a particular area, say not directly between the centre of the earth and the object, there will always be an area of mass with the exact amplitude and opposite angle such that the average force of gravity is directly towards the centre of mass (note, not the geometric centre). The bulge and centrifugal force is something I hadn't considered, and that clearly makes a difference - sort of. The centrifugal force reduces the net force exerted on the object on the surface, but it's not like it's actually reducing the force of gravity, it's just a different force. I'm just not convinced that the fact that the mass is distributed matters, if we assumed a stationary sphere. I'm also assuming symmetrical distribution of mass.
I just looked at Kahn's explanation. and find it far from satisfactory. He ignored buoyancy. If I use a scale to measure my weight it will be one thing in a vacuum, another in air (account for the weight of the displaced air) and another in water (displaced water). Air has mass because it has atoms, but if I put air on a scale (it's already there) I get zero.
As for center of mass, I'm with Trevor, much as I admire and learn from Dana Dorsett at every turn. Vectors help a lot. If we resolve the individual attraction vectors into components in the direction of gravity and perpendicular to it, the perpendicular ones sum to 0, meaning my fall direction lines up with the center of mass of the earth, and those in line sum correctly, by my calcs. If there was a tunnel through the center, my acceleration would be 0 (change direction) at the center.
A scale is an instrument with limitations. The fact that you'd get a different reading in water than in air simply illustrates the limitations of the instrument, it doesn't imply that the weight of the object is actually different in those mediums. In other words, the scale is not able to separate out the force of buoyancy from the force of weight.
One could use a vacuum chamber to fix the limitation. Or the next time you weigh yourself (in air), just add about .1 kg to what is indicated.
Great Article !
Thanks for sharing!
Log in or create an account to post a comment.
Sign up Log in