Heat loss calculus: solar heated siding and air space
I would like to discuss about the implications on heat loss calculations of temperature of exterior finish and its different layers (notably air space) and its effect on the delta T .
I have not found much info using the search, rather some mentions about the effect etc.. Maybe I am not using the correct terms to look it up?
So basically, when we are calculating the heat loss of an area using HDD or simply a specific time delta T, how is it affected?
A dark grey finish with a 3/4 air space under it should get pretty hot during day time when the sun is shining high…
can this be used to our advantage?
it is used in some calculators automatically?
Lastly, it comes to mind that one could use this to help with heat loss on any ~south oriented walls in north climates?
GBA Detail Library
A collection of one thousand construction details organized by climate and house part
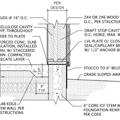
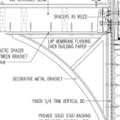







Replies
Jin,
Here are two articles on performing heat loss calculations:
How to Perform a Heat-Loss Calculation — Part 1
How to Perform a Heat-Loss Calculation — Part 2
You're right that the temperature of the siding is affected by how much sun the siding is exposed to, and to some extent by the color of the siding. However, the significance of these effects diminishes rapidly if the wall is well insulated. The effects are more noticeable in uninsulated walls.
The best reference work for calculating the R-value of air spaces is ASHRAE Fundamentals, which includes a table showing R-values for vertical and horizontal air spaces bounded by materials with different emissivities.
thanks sifu , i'll go through this tonight ... bonne journee :)
OK Sifu, had time go through the links ..but it was a "re do" for me...
But how much does the temperature of the exterior, that is readily absorbing energy from the sun,
affects the equation ??
When calculating heat loss , we are using IN and OUT deltaT , but if the outside temperature near the surface of the sheathing let's say, is temporarily raised by Xdegree from the sun,
does it temporarily change the deltaT in the equation equally ?
Jin,
Q. "When calculating heat loss , we are using IN and OUT deltaT, but if the outside temperature near the surface of the sheathing let's say, is temporarily raised by Xdegree from the sun, does it temporarily change the deltaT in the equation equally?"
A. Design heat loss calculations are made for worst case-conditions, when the outdoor temperature is coldest. These conditions occur between midnight and dawn. That's why design heat loss calculations never consider any solar contribution. After all, when the sun is shining, the heat loss is less than it is on a cold night.
Design heat loss conditions occur for only a few hours a year. During the heating season, the actual heat loss is almost always less than the design heat loss. After all, the outdoor air temperature is usually warmer than the design temperature. When the sun shines, many things happen. The siding on the south side of the house gets a little warmer. There is solar gain through the windows. These factors, plus warmer outdoor temperatures, certainly reduce the building's heat loss.
Martin i wasn't referring to "design heat loss" calculation necessairly,
but rather to all heat loss calculations ( be it instantaneous, or yearly energy use etc... )
sorry if it was not clear
Let me present a quick example out of nowhere, just so that you can verify if i am getting this correctly.
Let's assume a 55m2 south wall ( ~600sqft )
that has a U value or 0.28 ( ~us R20 )
with a design temp @ 20c @ a local HDD ( K ) of 4500
I would be tempted to make the following approximation :
55 x 0.28 = 15.4w of loss per K
sun heats up the siding and its air space by average of 33% ( this is out of nowhere ..sorry just for example )
for 3 hours /day
so 15.4W X ( 4500 - 33%) ( 24h /8 ) = ~ 140kw/h
( i know i can't divide the day time like this as temp is higher during day ..but just to get a very rough idea of what we are looking at ... the actual energy would be lower )
out of :
15.4 * 4500 *24 = 1600kw/h
Not that much impact , roughly maximum potential of 10$/year impact on this example.
But was fun guesstimating.
You think i got it all wrong ?
( sorry i'm really practicing my stuff here , this kind of headscratching helps me learn alot )
Then you would have the reverse effect during cooling seson i guess ?
which should be of less imapact because the delta T is less ??
still .. negates some of this very little impact.
Jin,
I haven't checked your calculations, but I'd just like to point out that this is a very complicated dynamic calculation. Very few energy modeling programs account for solar heating of siding on an hourly basis, but a few do. As far as I understand, WUFI is an example of a program that does.
I can't imagine any way that pencil-and-paper calculations will ever be useful here. This is a calculation that most be either modeled or ignored.
Sifu thanks for the input .. i understand fully that the exact implication has a much broader approach required for calculus ...
Wanted basically to verify if with a very "generalized approximation " i could determine the maximum importance in the global pictures
still i would like if someon could confirm that the temperature raise on the exterior surface of a wall has a direct impact using a changed deltaT in the heat loss formula ,
i tend to see the heat loss formula as a "2d" approximation and don't understand the impact
a surface temp would imply on a multi layered and multi material assembly depth.
Jin,
Q. "Still I would like if someone could confirm that the temperature raise on the exterior surface of a wall has a direct impact using a changed deltaT in the heat loss formula."
A. The answer is yes. That's why I wrote, in my previous answer, "When the sun shines, ... the siding on the south side of the house gets a little warmer. There is solar gain through the windows. These factors, plus warmer outdoor temperatures, certainly reduce the building's heat loss."
The temperature of the air in the air space depends on a huge number of factors, including the outdoor air temperature; the intensity of the sunlight (which is affected by the cloud cover and local pollution); the angle of the sunlight, which changes throughout the day as well as seasonally; and the rate of air movement in the air space (which depends on the size of the openings at the bottom of the wall and the top of the wall, the height of the wall, and the difference in the air temperatures at the bottom and top of the air space).
Once you measure all of those factors and enter them into your pencil-and-paper calculations, you'll have to re-measure them 5 minutes later... because they will have changed.
When these factors affect the temperature of the air in the rainscreen gap on the south side of your house, the same factors are absent on the north side of your house.
Sharpen your pencil, Jin. You've got a lot of figuring to do.
Or you can just let a computer program do it for you.